In ‘Cyclical Vector Fields and Seasonality,’ we saw that a rotational vector field could introduce seasonal patterns to prices over time, but it didn’t introduce stationary – ie, it didn’t result in a limiting distribution with a finite covariance matrix.
In 'Seasonality and Stationary with the ‘Drain’ Vector Field,’ we saw that this vector field could introduce both seasonality and stationary but at the cost of a continual dampening in the amplitude of the seasonal cycle. I ended that post by mentioning a solution to this conundrum.
In particular, we can take a trick from John Hull and Alan White, who modified the drift term in Vasicek’s one-factor interest rate model in order to fit their term structure model precisely to an observed yield curve. In particular, they started with the stochastic differential equation for the short rate assumed by Vasicek:
dr(t) = -k[r(t)-m] dt + v dw(t)
where dr(t) is the instantaneous change in the short rate, r(t), at time t
k is the speed with which r(t) reverts around m, its long-run mean
v scales the Wiener process, w(t), with instantaneous change dw(t).
And then they allowed the mean around which the short rate reverts to be a function of time, ie
dr(t) = -k[r(t)-m(t)] dt + v dw(t)
(See John Hull, Alan White; Pricing Interest-Rate-Derivative Securities, The Review of Financial Studies, Volume 3, Issue 4, 1 October 1990, Pages 573–592).)
In our case, the trick is to allow the mean around which the gasoline crack spread reverts to be a function of time and to allow the mean around which the diesel crack spread reverts to be another function of time.
The first graph below shows the RBOB-Brent crack futures curve as of the close on 14-Dec-18.
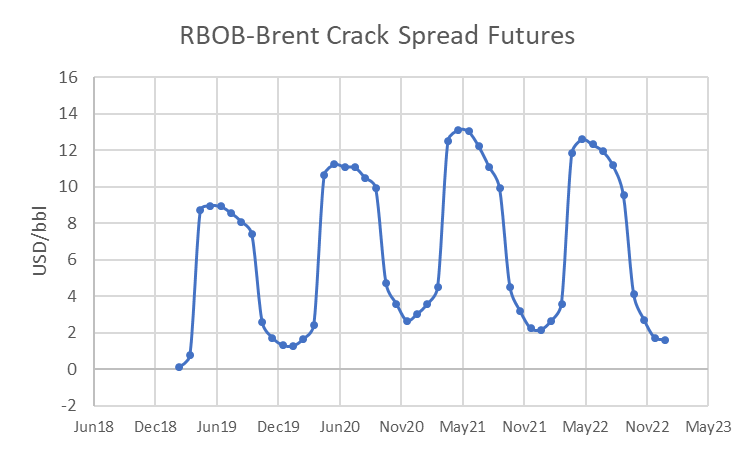
The next graph shows a discrete representation of the time-varying function used to adjust the mean for the RBOB-Brent crack spread (starting with October, the first month of the winter season).

The next graph shows the ULSD-Brent crack futures curve as of the close on 14-Dec-18.

The next graph shows a discrete representation of the time-varying function used to adjust the mean in this case.

Note that the time-varying mean for the RBOB-Brent crack spread, in particular, isn’t a continuous function of time, consistent with the fact that the change from the winter to summer specification takes place in mid-March, and the change from the summer to winter specification takes place in mid-September.
In this case, we’d expect to observe discontinuities in the unadjusted spot price series – but not in the adjusted spot price series. In particular, we’d expect the adjusted spot-price series to appear to be continuous functions of time (albeit with discrete observations).
Introducing seasonality with a time-varying mean is preferable to introducing seasonality via the transition matrix, for two reasons. First, this approach allows us to have seasonality with a consistent amplitude as well as stationarity – a combination we were having difficulty achieving via the transition matrix.
Second, by using a time-varying mean to capture the seasonality, we can retain maximum flexibility in the transition matrix (ie, maximum degrees of freedom) to capture the dynamics of the vector field in which the prices are embedded. In contrast, when we used the transition matrix to introduce seasonality, most of the degrees of freedom in the transition matrix were used to introduce the rotation and (in the second example) the push toward the origin accompanying the rotation.
So was the introduction of rotational vector fields on this blog a dead end? I don’t think so. I haven’t yet found an application in finance in which I’d prefer to capture a set of dynamics via cyclical behavior in the vector field corresponding to the transition matrix. But it’s useful to know the sorts of behaviors that can be captured by these vector fields. And it was an interesting way to introduce the concept of time-varying means – an idea we do use more frequently in practice.
Comments