
One of the statistical approaches most frequently used by financial analysts is regression analysis, as it allows comparisons of current values of a dependent variable to values that would be expected given the current value of an independent variable.
For example, the graph below shows values of front-month Brent crude oil futures on the horizontal axis and the CADUSD exchange rate (in US cents per Canadian dollar) on the vertical axis. Blue points represent daily data since 2000, while the red point represents current prices.

The graph also includes two regression lines. The orange line corresponds to the regression line obtained when the CADUSD exchange rate is presumed to be the dependent variable, while the green line corresponds to the regression line obtained when the crude oil futures price is presumed to be the dependent variable. (Both lines are estimated allowing for autocorrelation in the respective residual series.)
The difference between the two regression lines is due to the fact that the orange line is drawn to minimize the sum of squared vertical distances between the points and the line, whereas the green line is drawn to minimize the sum of squared horizontal distances between the points and the line.
Which regression line should we use? Well, that depends on our objective. If we want to calculate the current value of the CADUSD exchange rate that we would have expected given the current value of the Brent futures price, we should use the orange line. And if, instead, we want to calculate the current value of the Brent futures price that we would have expected given the current value of the CADUSD exchange rate, we should use the green line.
But what if we want to calculate the expected future value of the CADUSD exchange rate, conditional on the current values of both the CADUSD exchange rate and the Brent futures price? One approach would be to hold the value of the Brent futures price equal to its current value and to calculate the expected path of the residual with respect to the orange line, given that the residual tends to revert around a mean of zero with a speed we can estimate. But on what grounds would we assume that the Brent futures price would remain constant? Shouldn’t we expect its value to change over time as well?
And what if we want to calculate the expected future values of both variables – or of their spread – conditional on the current values of both the Brent price and the CADUSD exchange rate? Our regression analysis isn’t going to be of much help in this case, as it requires us to condition our calculations on knowledge of an independent variable.
As it happens, the multivariate Ornstein-Uhlenbeck process is an excellent model to use in this case. The variables are treated symmetrically in the MVOU model, eliminating the need to designate one of the variables arbitrarily as the dependent variable. The model takes autocorrelation into consideration by design. And it allows us to calculate conditional and unconditional expectations of any of the variables, at any horizon. And as we’ve noted before, the multivariate Ornstein-Uhlenbeck model allows us to capture horizon-dependent correlation – a useful characteristic in this case, given that the estimated correlation coefficient using daily changes is 0.39, using weekly changes is 0.48, using monthly changes is 0.52, using three-month changes is 0.55, and using levels is 0.9.
For brevity, we’ll define x to be the de-meaned CADUSD exchange rate, and we’ll define y to be the de-meaned Brent price. Then we can write stochastic differential equations for x and y of the form:
dx = [-ux – f(x- b*y)] dt + some diffusion term…
dy = [-vy – g(y-[x/b])] dt + some diffusion term…
where
u and v are the strengths with which x and y are attracted to their means (of zero) over the instantaneous time interval, dt
f is the strength with which x is attracted to b*y
g is the strength with which y is attracted to x/b.
For example, if b=2, and if f is positive, then there is a force tending to push x lower when x is greater than 2 y, and there is a force tending to push x higher when x is less than 2 y. Similarly, if g is positive, then there is a force tending to push y lower when y is greater than x/2, and there is a force tending to push y higher when y is less than x/2.
Using daily data since 4-Jan-00, the estimated value for b is 2.27, and the CADUSD exchange rate is estimated to revert around a mean of 90 US cents/CAD with a half-life of about three years. In contrast, the price of Brent exhibits almost no attraction toward its long-run mean. But it does exhibit a meaningful attraction (consistent with a half-life of just over four months) to the CADUSD exchange rate. The corresponding paths of expected values are shown along with the historical values in the next graph.

We also can calculate a path of expected values for one variable conditioned on a path of expected values for the other variables and on the current values of both variables. For example, let’s imagine that the path of expected values we associate with the Brent price corresponds to the current term structure of Brent futures prices. What would be the associated path of expected values for the CADUSD exchange rate, given our estimated model?
For this, we recall that the multivariate Ornstein-Uhlenbeck model has normal increments. And if we can calculate the expected values and covariances of these two variables to any horizon date, we can calculate the expected value of CADUSD conditional on Brent at that horizon date via the standard formula
E[x | y=z]=E[x] + (Cov[x, y]/Var[y]) (z-E[y])
Applying this formula using values for z that correspond to the current prices of Brent futures expiring in coming months produces paths of expected values shown in the next graph.
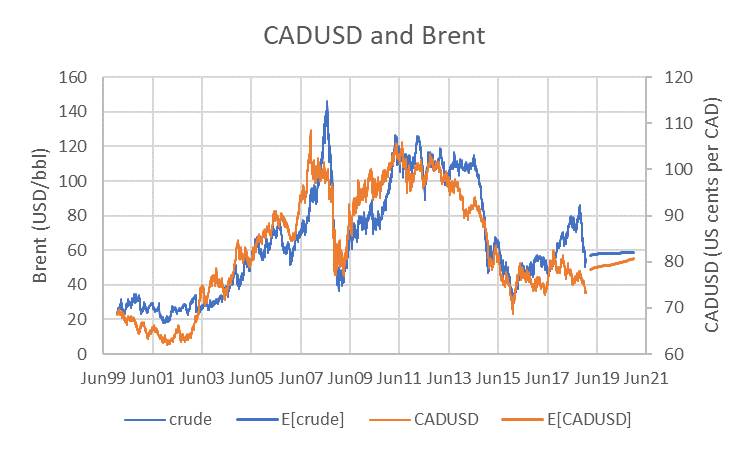
Keep in mind that the covariance between the Brent price and the CADUSD exchange rate is different at each horizon, as is the variance of the Brent price. As a result, the ratio of the covariance to the variance (the beta in the context of a traditional regression) is different for each horizon. In other words, just as we have horizon-dependent correlations, we also have horizon-dependent betas.
While horizon dependent correlations and betas require greater care to implement, they’re useful in that they allow us to reflect characteristics of the data that actually do depend on the time horizon. And the additional care required to implement the model is well worth the effort, given the ability of the model to address questions that are otherwise awkward, if not impossible, to address in the context of a traditional regression.
Comments